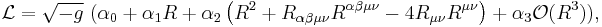Lovelock theory of gravity
In physics, Lovelock's theory of gravity (often referred to as Lovelock gravity) is a generalization of Einstein's theory of general relativity introduced by David Lovelock in 1971. It is the most general metric theory of gravity yielding conserved second order equations of motion in arbitrary number of spacetime dimensions  . In this sense, Lovelock's theory is the natural generalization of Einstein's General Relativity to higher dimensions. In dimension three and four (
. In this sense, Lovelock's theory is the natural generalization of Einstein's General Relativity to higher dimensions. In dimension three and four (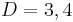 ), Lovelock's theory coincides with Einstein's theory, but in higher dimension both theories are different. In fact, for
), Lovelock's theory coincides with Einstein's theory, but in higher dimension both theories are different. In fact, for 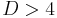 Einstein gravity can be thought of as a particular case of Lovelock gravity since the Einstein-Hilbert action is one of several terms that constitute the Lovelock action.
Einstein gravity can be thought of as a particular case of Lovelock gravity since the Einstein-Hilbert action is one of several terms that constitute the Lovelock action.
The Lagrangian of the theory is given by a sum of dimensionally extended Euler densities, and it can be written as follows
where 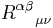 represents the Riemann tensor, and where the generalized Kronecker
represents the Riemann tensor, and where the generalized Kronecker  -function is defined as the antisymmetric product
-function is defined as the antisymmetric product
Each term 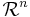 in
in 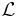 corresponds to the dimensional extension of the Euler density in
corresponds to the dimensional extension of the Euler density in 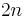 dimensions, so that these only contribute to the equations of motion for
dimensions, so that these only contribute to the equations of motion for 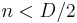 . Consequently, without lack of generality,
. Consequently, without lack of generality,  in the equation above can be taken to be
in the equation above can be taken to be 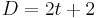 for even dimensions and
for even dimensions and 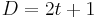 for odd dimensions.
for odd dimensions.
The coupling constants 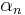 in Lagrangian
in Lagrangian 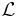 have dimensions of [length]
have dimensions of [length]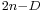 , although it is usual to normalize the Lagrangian density in units of the Planck scale
, although it is usual to normalize the Lagrangian density in units of the Planck scale 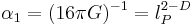 . Expanding the product in
. Expanding the product in 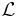 , the Lovelock's Lagrangian takes the form
, the Lovelock's Lagrangian takes the form
where one sees that coupling 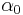 corresponds to the [[cosmological constant]]
corresponds to the [[cosmological constant]] 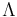 , while
, while 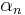 with
with 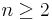 are coupling constants of additional terms that represent ultraviolet corrections to Einstein theory, involving higher order contractions of the Riemann tensor
are coupling constants of additional terms that represent ultraviolet corrections to Einstein theory, involving higher order contractions of the Riemann tensor 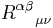 . In particular, the second order term
. In particular, the second order term 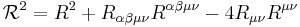 is precisely the quadratic Gauss–Bonnet term, which is the dimensionally extended version of the four-dimensional Euler density.
is precisely the quadratic Gauss–Bonnet term, which is the dimensionally extended version of the four-dimensional Euler density.
Due to the fact that Lovelock action contains, among others, the quadratic Gauss–Bonnet term (i.e. the four-dimensional Euler characteristic extended to  dimensions), it is usually said that Lovelock theory resembles string theory inspired models of gravity. This is because such quadratic term is present in the low energy effective action of heterotic string theory, and it also appears in six-dimensional Calabi–Yau compactifications of M-theory. In the mid 1980s, a decade after Lovelock proposed his generalization of the Einstein tensor, the physicists began to discuss the quadratic Gauss–Bonnet term of Lovelock action within the context of string theory, with particular attention on its property of being free of ghost about the Minkowski space. The theory is known to be free of ghosts about other exact backgrounds as well, e.g. about one of the branches of its spherically symmetric solution found by Boulware and Deser in 1985. In general, Lovelock's theory represents a very interesting scenario to study how the physics of gravity results corrected at short distance due to the presence of higher order curvature terms in the action, and in the mid 2000s the theory was considered as a testing ground to investigate the effects of introducing higher-curvature terms in the context of AdS/CFT correspondence.
dimensions), it is usually said that Lovelock theory resembles string theory inspired models of gravity. This is because such quadratic term is present in the low energy effective action of heterotic string theory, and it also appears in six-dimensional Calabi–Yau compactifications of M-theory. In the mid 1980s, a decade after Lovelock proposed his generalization of the Einstein tensor, the physicists began to discuss the quadratic Gauss–Bonnet term of Lovelock action within the context of string theory, with particular attention on its property of being free of ghost about the Minkowski space. The theory is known to be free of ghosts about other exact backgrounds as well, e.g. about one of the branches of its spherically symmetric solution found by Boulware and Deser in 1985. In general, Lovelock's theory represents a very interesting scenario to study how the physics of gravity results corrected at short distance due to the presence of higher order curvature terms in the action, and in the mid 2000s the theory was considered as a testing ground to investigate the effects of introducing higher-curvature terms in the context of AdS/CFT correspondence.
See also
References
- D. Lovelock, The Einstein tensor and its generalizations, J. Math. Phys. 12 (1971) 498.
- D. Lovelock, The four-dimensionality of space and the Einstein tensor, J. Math. Phys. 13 (1972) 874.
- Navarro, A. and Navarro, J., Lovelock's theorem revisited, J. Geom. Phys. 61 (2011) 1950-1956. (PDF)
- B. Zwiebach, Curvature Squared Terms and String Theories, Phys. Lett. B156 (1985) 315.
- D. Boulware and S. Deser, String Generated Gravity Models, Phys. Rev. Lett. 55 (1985) 2656.
|
|||||||||
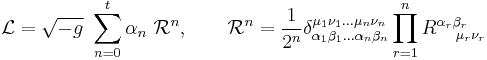
![\delta _{\alpha _{1}\beta _{1} \cdots \alpha _{n}\beta _{n}}^{\mu _{1}\nu
_{1}...\mu _{n}\nu _{n}}=\frac{1}{n!}\delta _{\lbrack \alpha _{1}}^{\mu
_{1}}\delta _{\beta _{1}}^{\nu _{1}}\cdots \delta _{\alpha _{n}}^{\mu
_{n}}\delta _{\beta _{n}]}^{\nu _{n}}.](/2012-wikipedia_en_all_nopic_01_2012/I/2aebaa1ae7a53fcb04f86c9d5b68146f.png)